Fungsi Komposisi

 

Fungsi Komposisi: Definisi, Invers, dan Contoh Soal

 

Kalian pasti pernah menemukan lebih dari 1 fungsi matematika.

Lalu apa yang bisa dilakukan dengan 2 atau lebih fungsi matematika tersebut?

Nah dari 2 atau lebih fungsi matematika tersebut, kalian bisa menurunkan fungsi baru yang merupakan hasil dari operasi fungsi komposisi.

Lalu apakah fungsi komposisi itu?

Mari kita bahas lebih lanjut mengenai fungsi komposisi.

Definisi Fungsi Komposisi

Operasi fungsi komposisi merupakan operasi yang digunakan pada minimal 2 fungsi untuk melahirkan sebuah fungsi yang baru.

Notasi dari fungsi komposisi adalah ‘o’ atau sering disebut dengan ‘bundaran’ atau ‘komposisi’

Contohnya apabila terdapat 2 fungsi yaitu f(x) dan g(x) maka (f o g) (x) atau dibaca fungsi f bundaran g maka dapat dikerjakan dengan cara memasukkan fungsi g ke dalam fungsi f.

Lebih jelasnya lihat di gambar berikut

Rumus Fungsi Komposisi

Secara umum rumus fungsi komposisi adalah

Diketahui terdapat 2 fungsi yaitu fungsi f(x) dan fungsi g(x), maka fungsi h(x) yang didefinisikan sebagai h(x)=(f o g)(x) dapat dicari dengan cara

h(x) = (f o g)(x) = f(g(x))

Ilustrasinya adalah jika terdapat fungsi f dan g yang merupakan mesin yang bekerja secara beriringan.

Fungsi g mendapatkan input berupa (x) yang diproses oleh mesin f kemudian outputnya berupa g(x).

Kemudian g(x) menjadi input untuk diolah mesin f sehingga diperoleh output berupa f(g(x)).

Komposisi Fungsi

Ada istilah lain mengenai fungsi komposisi yang patut kita ketahui, yaitu komposisi fungsi.

Komposisi fungsi adalah penggabungan operasi dari dua fungsi yang secara berurutan lalu menghasilkan sebuah fungsi baru.

Untuk notasinya, notasi dari komposisi fungsi sama dengan notasi fungsi komposisi yaitu ‘o’ atau ‘bundaran’.

Sifat dari Komposisi Fungsi

Terdapat beberapa sifat dari komposisi fungsi, diantaranya :

·         Tidak bersifat komutatif : (f o g)(x) ≠(g o f)(x)

·         Bersifat assosiatif : ((f o g) o h)(x) = (f o (g o h))(x)

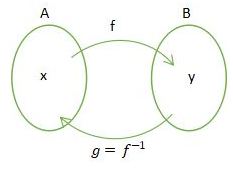
Fungsi Invers

Jika fungsi f merupakan fungsi yang memetakan dari A ke B dan memiliki relasi dengan fungsi g yang memetakan B ke A, maka fungsi g merupakan invers atau balikan dari f dan ditulis f^-1 atau g = f^-1 Jika g merupakan fungsi, maka g = f^-1 disebut fungsi invers atau fungsi balikan.

Untuk lebih jelasnya lihat gambar berikut

Cara Mencari Invers dari Suatu Fungsi

Mencari invers fungsi y=f(x) dapat dicari dengan cara berikut:

1.       Ubah persamaan y=f(x) ke dalam bentuk x=f(y)

2.      Ubah x dengan  f^-1(y) sehingga  f(y) =  f^-1(y)

3.      ubah y dengan x kemudian diperoleh invers dari f(x) berupa  f^-1

Contoh Soal Fungsi Komposisi

1. Jika terdapat fungsi f(x)=5x+1 dan diketahui bahwa (f o g) (x) = 10x+6 maka g(x) adalah

Pembahasan

(f o g)(x) = 10x + 6

f(g(x)) = 10x + 6

5(g(x))+1 = 10x + 6

5(g(x)) = 10x + 5

g(x) = 2x + 1

Jadi fungsi g(x) yang dicari adalah g(x) = 2x + 1

2. Berdasarkan soal No.1 tentukan invers dari g(x)

Pembahasan

y=g(x)

y=2x+1

2x=y-1

x=(y-1)/2

 g^-1(y) = (y-1)/2

 g^-1(x) = (x-1)/2

Jadi fungsi g(x) inversnya adalah  g^-1(x) = (x-1)/2