Integral:
Pengertian, Macamnya, Rumus Lengkap
Artikel kali
ini akan membahas mengenai integral.
Sebelum
mempelajari materi integral, sebaiknya kalian memahami terlebih dahulu materi
diferensial atau turunan.
Sudahkah
kalian belajar mengenai diferensial atau turunan?
Materi turunan
(diferensial) akan digunakan dalam penyelesaian integral. Untuk memahami apa
itu integral, pelajari materi di bawah ini.
Definisi Integral
Integral secara sederhana dapat
disebut sebagai invers (kebalikan) dari operasi turunan. Integral dibedakan
menjadi dua yaitu integral tak tentu dan integral tentu.
Integral tak tentu merujuk pada
definisi integral sebagai invers (kebalikan) dari turunan, sedangkan integral
tentu didefinisikan sebagai jumlahan suatu daerah yang dibatasi kurva atau
persamaan tertentu.
Pada bagian di bawah akan
dijelaskan contoh penerapan integral.
Contoh Penerapan Integral
Integral dimanfaatkan dalam
berbagai bidang. Pada bidang matematika dan teknik, integral digunakan untuk
menghitung volume benda putar dan luasan pada kurva.
Pada bidang fisika, pemanfaatan
integral digunakan untuk menghitung dan menganalisis rangkaian arus listrik,
medan magnet, dan lainnya.
Berikut akan dijelaskan mengenai
rumus integral dasar/sederhana.
Rumus Integral
Misalkan terdapat suatu fungsi sederhana axn. Integral dari fungsi tersebut
adalah
Rumus Integral
Keterangan:
·
k : koefisien
·
x : variabel
·
n : pangkat/derajat dari variabel
·
C : konstanta
Misalkan terdapat suatu fungsi f(x). Jika kita akan menentukan
luas daerah yang dibatasi oleh grafik f(x) maka dapat ditentukan dengan
dengan a dan b merupakan gari vertikal atau batas luasan
daerah yang dihitung dari sumbu-x. Misalkan integral dari f(x) disimbolkan
dengan F(x) atau jika dituliskan
maka
Keterangan:
·
a, b : batas atas dan
batas bawah integral
·
f(x) : persamaan kurva
·
F(x) : luasan di bawah
kurva f(x)
Sifat Integral
Beberapa sifat integral yaitu
sebagai berikut.
Integral Tak Tentu
Seperti yang telah dijelaskan
pada bagian sebelumnya, integral tak tentu merupakan suatu kebalikan dari
turunan. Kalian dapat menyebutnya sebagai anti turunan atau antiderivative.
Integral tak tentu dari suatu
fungsi menghasilkan fungsi baru yang belum memiliki nilai yang tentu karena
masih terdapat variabel dalam fungsi baru tersebut. Bentuk umum integral
tentu
Rumus Integral
Tak Tentu
Keterangan:
·
f(x) : persamaan kurva
·
F(x) : luasan di bawah kurva f(x)
·
C : konstanta
Contoh integral tak tentu:
Integral Tentu
Integral tentu didefinisikan
sebagai jumlahan suatu daerah yang dibatasi kurva atau persamaan tertentu.
Berbeda dari integral tak tentu,
integral tentu memiliki nilai tertentu karena batas yang ditentukan sudah
jelas.
Secara umum, integral tentu
didefinisikan sebagai
Rumus Integral Tentu
Keterangan:
·
f(x) : persamaan kurva
·
a, b : batas bawah dan batas atas integral
·
F(b), F(a) : nilai integral untuk x = b dan x = a.
Integral Pecahan
Fungsi pecahan dapat
didefinisikan sebagai f(x)/g(x). Penyelesaian integral fungsi pecahan dapat
dilakukan dengan memecah fungsi yang kompleks menjadi beberapa fungsi yang
lebih sederhana. Perhatikan contoh berikut.
(A + B) x + B – A = 1
Sehingga
B – A = 1 , dan A + B = 0
Didapatkan B = ½ dan A = – ½
Maka, dengan menggunakan sifat integral diperoleh
= ½ (- ln |x + 1| + ln |x – 1| + C1)
= – ½ ln |x + 1| + ½ ln |x – 1| + C, dengan C = ½ C1
Selanjutnya akan dibahas
mengenai integral eksponensial.
Integral Eksponensial
Fungsi eksponensial biasanya dinotasikan dengan ex. Beberapa konsep dasar yang
harus dipelajari dalam integral eksponensial yaitu
Rumus Integral Exponensial
Keterangan:
·
ex, ekx : fungsi eksponensial
·
C :
konstanta
Selanjutnya akan dibahas
mengenai integral substitusi.
Integral Substitusi
Beberapa permasalahan atau
integral suatu fungsi dapat diselesaikan dengan integral substitusi jika
terdapat perkalian fungsi dengan salah satu fungsi merupakan turunan fungsi
yang lain.
Perhatikan contoh berikut.
Kita misalkan U = ½ x2 + 3 maka
dU/dx = x
Sehingga x dx = dU
Persamaan integral substitusinya menjadi
= -2 cos U + C = -2 cos ( ½ x2 + 3) + C
Berikutnya akan dijelaskan
mengenai integral parsial.
Integral Parsial
Integral parsial biasa digunakan
untuk menyelesaikan integral dari perkalian dua fungsi. Secara umum, integral
parsial didefinikan dengan
Rumus Integral Parsial
Keterangan:
U, V :
fungsi
dU, dV : turunan dari fungsi U dan turunan dari fungsi V
Tabel Integral
Berikut akan disajikan beberapa
bentuk integral tak tentu yang lain.
|
Integral fungsi |
Hasil integral |
|
|
-cos x + C |
|
|
sin x + C |
|
|
ln |sec x| + C |
|
|
arc sin x + C |
|
|
arc tan x + C |
|
|
arc sec x + C |
|
|
cosh x + C |
|
|
sinh x + C |
Coba kerjakan soal di bawah ini.
Contoh Soal Integral
Selesaikan integral berikut.
Pembahasan
1/(x2 – x + 6) = 1/((x – 3)(x + 2)) = A/(x – 3) + B/(x +
2)
A(x + 2) + B
(x – 3) = 1
(A + B) x + 2A
– 3B = 1
Diperoleh A =
1/5 dan B = – 1/5
= 1/5 (ln |x – 3| + C1 – ln |x + 2| – C2) = 1/5 ln |x –
3| – 1/5 ln |x + 2| + C, dengan C = 1/5 C1 – 1/5 C2
Misal:
u = x maka du
= dx
Sehingga
Misal :
u = cos x maka
du = – sin x, dengan menggunakan konsep integral substitusi diperoleh:
1/3 x3 + 3x + C dengan batas atas 2 dan batas bawah 1, sehingga:
= (1/3 (2)3 + 3 (2)) – (1/3 (1)3 + 3 (1))
= (8/3) + 6 –
1/3 – 3
= 16/3
Apa yang sudah kalian pelajari mengenai
integral.
Kesimpulan
·
Integral secara sederhana dapat disebut sebagai invers
(kebalikan) dari operasi turunan.
·
Integral dibedakan menjadi dua, yaitu integral tak tentu dan
integral tentu.
·
Beberapa bentuk dan teknik penyelesaian integral yaitu
·
Integral pecahan
·
Integral eksponensial
·
Integral substitusi
·
Integral parsial
·
Dengan menerapkan sifat-sifat integral akan lebih mudah dalam
menyelesaikan integralnya.
Demikian yang dapat disampaikan dalam artikel ini, semoga
bermanfaat.


















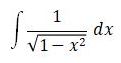












Tidak ada komentar:
Posting Komentar